- Was ist die Finite Elemente Methode (FEM)?
- Funktionsweise und Grundlade der Finite Elemente Methode
- FEM-Simulation: Anwendung der FEM
Was ist die Finite Elemente Methode (FEM)?
Bei der Finiten Elemente Methode (kurz: FEM) handelt es sich um ein nummerisches Berechnungsverfahren zur Lösung strukturmechanischer, mathematisch physikalischer oder chemischer Modelle beziehungsweise Problemstellungen. Von allgemeinem Maschinenbau und Fahrzeugbau über die Elektroindustrie und Optik hin zur Chemischen Industrie oder der Reaktorsicherheit. Die möglichen Einsatzgebiete sind groß und vielfältig.
Geschichte der FEM
Als Vorgänger der FEM kann die 1926 von Ostenfeld veröffentlichte Deformationsmethode für Stäbe und Balken gesehen werden, bei der als Unbekannte Größen nur die Knotenverschiebungen und -verdrehungen auftreten. Die entscheidenden Fortschritte für die FEM waren als 1960 die Verbindung zwischen den einfachen Methoden der Stabstatik zu den Variationsprinzipien der Statik, dem Prinzip der virtuellen Kräfte und dem Prinzip der virtuellen Verrückungen gezogen wurde. In den 1980er Jahren wurde die FEM schließlich verstärkt in der Mathematik bezüglich Konvergenz und Genauigkeit untersucht.
Zum Einsatz kommt die FEM Finite Elemente Methode heute meist in Form von FEM-Simulations-Software, wenn ein Berechnungsmodell sich händisch nicht mehr lösen lässt.

Bild 1: Vernetzung eines Werkstückes sowie des Werkzeuges
Funktionsweise und Grundlage der Finite Elemente Methode
Grundlage für die FEM ist die Diskretisierung für das zu berechnende Gebiet. Dies umschreibt die Unterteilung des Gesamtgebietes in eine endliche Zahl kleinerer (finiter) Elemente. Dadurch kann bei der Finiten Elemente Methode ein durch Differentialgleichungen beschriebenes Problem, das analytisch nicht lösbare ist, in ein algebraisches Problem umgewandelt werden. Die Genauigkeit der späteren Rechenergebnisse hängt dabei direkt von der Größe der gewählten Elemente ab, wobei eine zu feine Unterteilung im späteren Verlauf zu einem erheblich höheren Rechenaufwand führt. Bei 2D-Gebieten werden für die finiten Elemente Dreiecke oder Vierecke verwendet, während bei 3D-Gebieten hauptsächlich Quader- oder Tetraederelemente genutzt werden. Die das Element definierenden Randpunkte werden als Knoten bezeichnet.
Für diese gering komplexen Elemente kann bei der Finite Elemente Methode das jeweilige physikalische Verhalten mithilfe von Ansatzfunktionen (Differentialgleichungen) ausreichend genau repräsentiert werden. Höhere Ansatzfunktionen liefern hier genauere Ergebnisse erfordern gleichzeitig aber auch einen erhöhten Rechenaufwand. Das Reagieren einzelner finiter Elemente auf Einflüsse und Randbedingungen sowie das Fortpflanzen verschiedener Größen durch Reaktionen der Elemente untereinander ermöglichen ein Rückschluss auf das Verhalten des Gesamtbereiches. Dabei ist es erforderlich, dass die Ansatzfunktionen abhängig vom Problem eine Stetigkeit der Zustandsgrößen gewährleisten, was insbesondere an den Elementenübergängen aufwendiger ist. Alle Bedingungen und Funktionen werden entsprechend in einem Gleichungssystem zusammengefasst, welches gelöst werden kann.
Innerhalb der Lösung des aufgestellten Gleichungssystems können verschiedene Näherungsverfahren zum Einsatzkommen. Vom Prinzip der virtuellen Verrückung über das Verfahren von Ritz, die Methode der gewichteten Residuen hin zum Galerkin Verfahren.
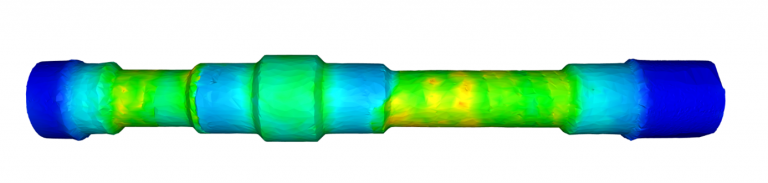
Bild 2: Verteilung des Umformgrades des gewalzten Werkstückes
FEM-Simulation: Anwendung der FEM
Die FEM-Simulation stellt bei der Anwendung dieser Methode ein zentrales Element dar. Grund dafür ist das mithilfe von FEM-Simulationssoftware und Computern sich komplexe Probleme mit relativ hoher Genauigkeit berechnen lassen. Dadurch können in der Umformtechnik beispielsweise aufwendige Vorversuche vermieden und die Entwicklungszeit für Produkte und Prozesse verkürzt werden. Um beispielsweise. im Rahmen der Produktentwicklung die Festigkeit von Bauteilen oder Baugruppen zu prüfen, werden FEM-Analysen für strukturmechanische Analysen eingesetzt. Auch Topoliegieopimierungen können auf Basis von FEM-Simulationen durchgeführt werden. Die FEM Simulation ist dabei stets nach den folgenden drei Punkten aufgebaut:
• Das als CAD konstruiertes Bauteil wird zunächst in ein kompatibles Dateiformat exportiert (z.B. STEP), um anschließend im Präprozessor weiter vorbereitet zu werden. Neben einer geeigneten Vernetzung des Bauteils müssen für die FEM Randbedingungen wie beispielsweise Lasten, Temperaturen oder Beschleunigungen festgelegt werden. Sind für den zu simulierenden Prozess weitere Körper wie zum Beispiel Werkzeuge erforderlich, so müssen diese ebenfalls vernetzt werden und Kontaktbedingungen zwischen allen Parteien definiert werden.
• Im zweiten Schritt der FEM wird das Gleichungssystem, welches sich aus dem im Präprozessor aufgestellten Prozess ergibt mit dem Solver näherungsweise gelöst. Dadurch werden die verschiedenen Einflüsse auf die einzelnen Elemente berechnet.
• Mithilfe des Postprozessors wird anschließend die Auswertung der Ergebnisse durchgeführt. Durch geeignete Farbbereiche können zusätzlich verschiedene Ergebnisgrößen (Temperaturen, Spannungen, Verschiebungen usw.) über den gesamten Bereich visuell dargestellt werden und so für folgende Interpretationen genutzt werden.
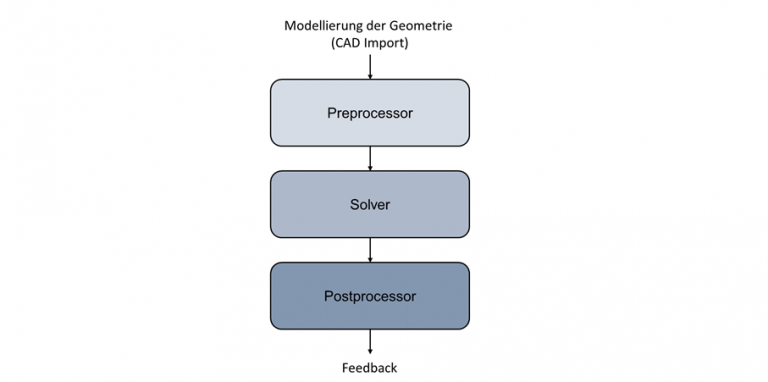
Bild 3: Schematischer Ablauf einer FEM Simulation
Innerhalb jeder dieser Phase können Fehler gemacht werden, die die Genauigkeit der Ergebnisse stark negativ beeinflussen können. Angefangen von einer nicht korrekten Problemanalyse über eine falsch gewählte Vernetzung hin zu stark vereinfachten Randbedingungen. Außerdem ist es für den auf der Finiten Elemente Methode basierenden Prozess entscheidend, dass keine unzureichenden Werkstoffkennwerte verwendet werden.
Umsetzung der Finite Elemente Methode
Um diese Fehler möglichst zu vermeiden und das volle Anwendungspotential von FEM-Software nutzen zu können, bedarf es viel fachlicher Kompetenz und Erfahrung. Darüber hinaus ist die notwendige Software mit entsprechenden Anschaffungskosten verbunden. Insofern ist es durchaus sinnvoll einen externen Dienstleister hinzuzuziehen. Das IPH Hannover bietet beispielsweise Schulungen zu FEM-Simulationen oder auch die direkte Bearbeitung eines Projektes an. Im Bereich der Umformtechnik führen wir für Ihr Bauteil und den entsprechenden Umformprozess eine Analyse des Ist-Zustands durch und legen mittels FEM-Software einen optimierten Prozess aus. Entsprechende Ergebnisse und die Auswertung der Simulationsergebnisse bereiten wir anschließend in einer plattformunabhängigen nutzbaren Form für sie auf (z.B. Excel). Für Sie ergeben sich so genaue Prozesskenntnisse auch ohne physische Versuche, eine aufwandsarme Prüfung alternativer Umformparameter (z.B. Temperatur, Material, Umformschritte etc.) und die Möglichkeit die Ergebnisse anschließend im realen Versuch verifizieren zu lassen. Im Rahmen des Prozesse der Produkt- und Prototypenentwicklung bietet das IPH FEM-Analysen zur strukturmechanischen Untersuchung und Analyse sowie weitere Beratung und Unterstützung bei der Finite Elemente Methode (FEM) an.



